数据分析与挖掘(二)分类模型实战
Published:
分类预测问题与回归预测问题不同。分类是预测一个离散类标签的任务。回归是预测一个连续量的任务。
分类和回归的算法之间有一些重叠。 例如:分类算法可以预测一个连续的值,但这个连续的值是以一个类标签的概率形式出现的。回归算法可以预测一个离散的值,但这个离散的值是以整数形式存在的。一些算法在稍作修改后可以同时用于分类和回归,如决策树和人工神经网络。有些算法不能或不容易用于两种问题类型,如用于回归预测建模的线性回归和用于分类预测建模的逻辑回归。重要的是,我们评估分类和回归预测的方式各不相同,并不重合,例如。分类预测可以用准确性来评估,而回归预测则不能。回归预测可以使用均方根误差进行评估,而分类预测则不能。接下来介绍分类任务中最常见的二分类和多分类。
二分类
我们指定一个二元分类问题,其中两个类别之间存在明确的线性边界。对于此类问题,诸如逻辑回归、线性判别分析(LDA)和二次判别分析(QDA)等技术是最广泛使用的算法。
线性判别分析(LDA)是一种非常常见的用于监督分类问题的技术。让我们一起了解什么是LDA,它是如何工作的。线性判别分析是一种降维技术,在机器学习和模式分类应用中作为预处理步骤使用。降维技术的主要目标是通过将特征从高维空间转换到低维空间,从而去除冗余和依赖性的特征来降低维度。顾名思义,降维技术减少了维度的数量,即在保留尽可能多的信息的同时,对数据集中的变量进行调整。
LDA分类依靠的是贝叶斯定理,该定理中的后验概率为
$P\left( Y | X \right) = \frac{P(X|Y)P(Y)}{P(X)}$
我们可以把X属于每个类别的概率与每个类别中的X的概率联系起来。因为我们希望上述公式易于计算,所以我们挑选了一个具有良好数学特性的概率密度函数——正态分布。
$N\left( \mu,\sigma \right) = \frac{1}{\sqrt{2\pi}}e^{- \frac{1}{2}{(\frac{X - \mu}{\sigma})}^{2}}$
这是LDA的一个关键假设。如果输入变量来自近似的正态分布,那么该技术的效果会更好。将正态分布代入并最大化后验概率即可求得LDA的参数估计。
LDA的步骤:
(1)计算数据集中不同类别的d维平均向量,其中d是特征空间的维度。
(2)计算类间和类内散度矩阵。
(3)计算散度矩阵的特征向量和相应的特征值。
(4)选择对应于前k个特征值的k个特征向量,形成一个维度为d × k的变换矩阵。
(5)通过变换矩阵将d维的特征空间X变换为k维的特征空间Xlda。
这里使用的数据集是UCI机器学习资源库中公开的银行票据认证数据集。数据集中的属性是
var: 小波变换图像的方差(连续)。
skewness: 小波变换图像的偏度(连续)。
curtosis: 小波变换图像的曲率(连续)。
entropy: 图像的熵(连续)。
class: 类别(整数)(0-不真实,1-真实)。
该数据集共包含1372个实例,其中762个为非真实票据,610个为真实票据。使用单变量和多变量图,属性的数据分布如下:
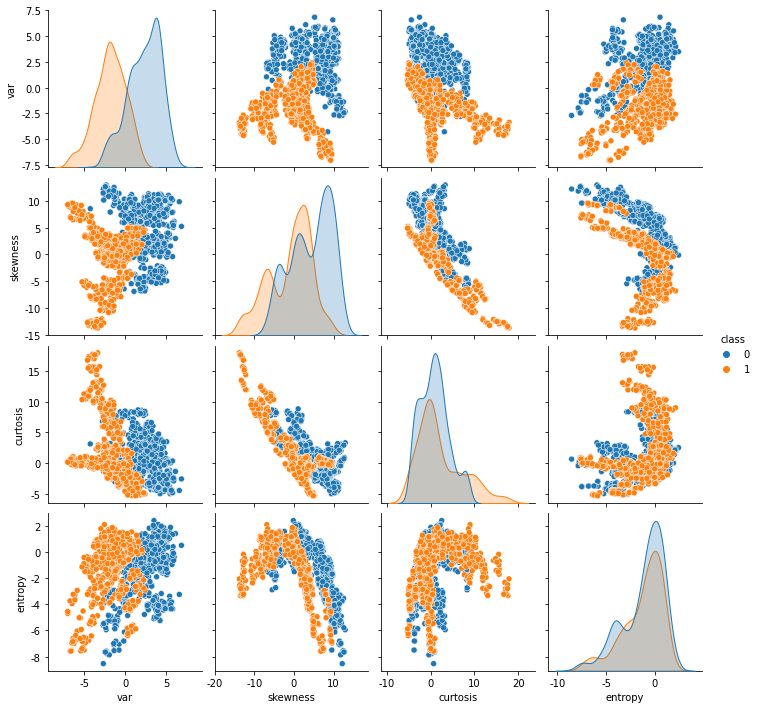
银行票据认证数据集变量分布图
现在,我们将计算两类的4维平均向量(维数=特征的数量)。与主成分分析(PCA)不同,LDA中不需要对数据进行标准化处理,因为它不会影响输出。标准化对LDA的主要结果没有影响的原因是,LDA分解的是类内协方差和类间协方差之间的比例,而不是协方差本身的大小(像PCA那样)。
下一步是计算类内散度矩阵和类间散度矩阵。我们的目标是最小化类内距离,最大化类间距离。核心代码如下:
1. SW = np.zeros((4,4))
2. **for** i **in** range(1,4): #2 is number of classes
3. per_class_sc_mat = np.zeros((4,4))
4. **for** j **in** range(df[df["class"]==i].shape[0]):
5. row, mv = df.loc[j][:4].reshape(4,1), mean_vec[i].reshape(4,1)
6. per_class_sc_mat += (row-mv).dot((row-mv).T)
7. SW += per_class_sc_mat
8. **print**('within-class Scatter Matrix:\n', SW)
9. overall_mean = np.array(df.drop("class", axis=1).mean())
10. SB = np.zeros((4,4))
11. **for** i **in** range(2): #2 is number of classes
12. n = df[df["class"]==i].shape[0]
13. mv = mean_vec[i].reshape(4,1)
14. overall_mean = overall_mean.reshape(4,1) # make column vector
15. SB += n * (mv - overall_mean).dot((mv - overall_mean).T)
16. **print**('between-class Scatter Matrix:\n', SB)
接下来,我们需要解决类间散度矩阵求逆和类间散度矩阵的广义特征值问题,以获得线性判别子。我们需要选择对应于前k个特征值的前k个特征向量。在这里,我们取前2个特征值对应的特征向量,以达到可视化的目的。但我们将属于最大特征值的特征向量保留了近100%的方差,所以我们也可以舍弃其他3个。我们将四维特征空间X转换为二维特征子空间Xlda。带有这两个变量的数据分布现在看起来如下。
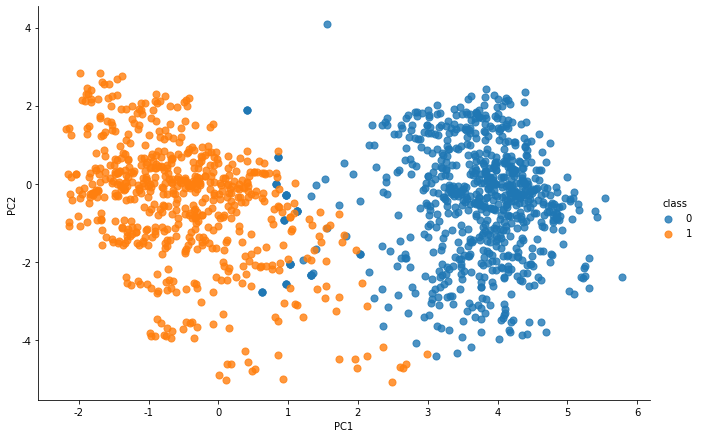
数据压缩后分布图
接着进行LDA模型的训练拟合,代码如下:
1. **from** sklearn.discriminant_analysis **import** LinearDiscriminantAnalysis
2. model = LinearDiscriminantAnalysis(n_components=3)
3. X_lda = model.fit_transform(X, y)
我们可以得到模型的评价指标:
| 类别 | 精度 | 召回率 | F1值 | 支持量 |
|---|---|---|---|---|
| 0 | 1 | 0.96 | 0.98 | 762 |
| 1 | 0.95 | 1 | 0.97 | 610 |
| 平均/总和 | 0.98 | 0.98 | 0.98 | 1372 |
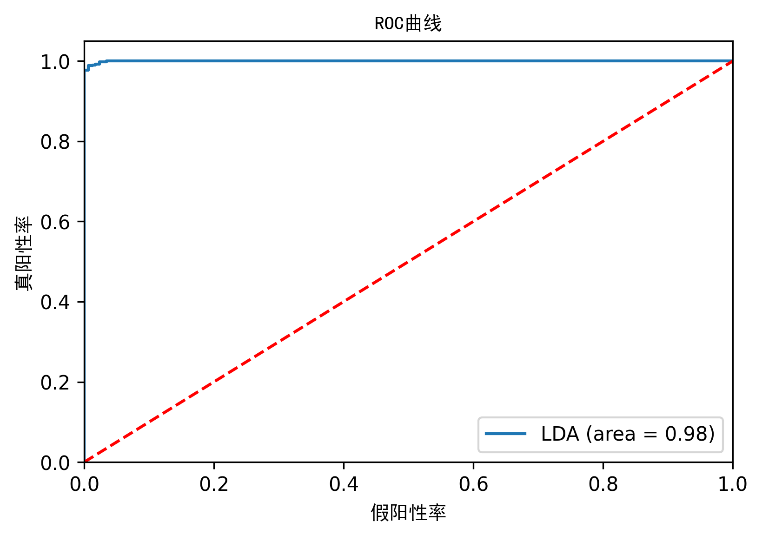
线性判别分析的ROC曲线
在这里,我们可以看到,从LDA实现中也可以看出,只有一个主成分也能够非常准确地区分出类别。
多分类
现实中常遇到的多分类任务,有些二分类任务可以直接扩展到多分类任务上。例如上节所介绍的LDA。读者可自行尝试将LDA模型扩展至多分类任务上。本节将介绍一个重点的多分类学习器,即决策树。
决策树是机器学习的一个广泛领域,涵盖了分类和回归。在决策分析中,可以用决策树来直观、明确地表示决策和决策的制定。顾名思义,它使用了一个树状的决策模型。虽然它是数据挖掘中常用的工具,用于推导出达到特定目标的策略,但它也广泛用于机器学习。
作为最流行的经典机器学习算法之一,决策树的可解释性比其他算法要直观得多。决策树(DT)是一种用于分类和回归的非参数化监督学习方法。目标是创建一个模型,通过学习从数据特征推断出的简单决策规则来预测目标变量的值。
这一节中我们将向你展示实现决策树分类模型的整个工作流程。一个典型的机器学习任务的工作流程通常从数据整理开始,因为我们最初得到的数据往往不能直接使用。这就是所谓的原始数据。
泰坦尼克号的生存数据集在数据科学领域很有名。决策树的解决方案可以很好地预测存活率,我们使用这个数据集作为一个例子来训练我们的决策树分类模型。
数据集原始数据可以从Kaggle1中获取。数据集的说明,包括变量、训练/测试集等。 可在页面下方链接中找到,并可下载数据集。在实践中,一个特定的原始数据集的所有信息可能不够清晰。
我们使用探索性数据分析(EDA)对数据进行清洗和描述。EDA的结果不直接用于模型训练,但它不能被忽视。我们需要详细了解数据集,以便于数据清理和特征选择。这里我将展示一些基本的和常用的EDA技巧。
我们对我们的数据框架进行分析。只需调用数据框的info()函数,特征统计:检查特征的统计也是非常重要的。pandas的数据框架也可以非常容易地为我们做到这一点。describe()函数会自动选择数字特征,并为我们计算出它们的统计数据。
Survived: 是否存活(0=否,1=是)。
Pclass: 船票舱位。
Sex: 性别。
Age: 年龄。
SibSp: 在泰坦尼克号上的兄弟姐妹/配偶的数量。
Parch: # 泰坦尼克号上的父母/子女人数。
Ticket: 船票数量。
Fare: 乘客票价。
Cabin: 船舱号。
Embarked: 登岸港(C=瑟堡,Q=皇后镇,S=南安普敦)。
在实践中,你可能需要通过EDA做更多的分析工作,比如在直方图中绘制特征以查看它们的分布,或者得到相关矩阵等等。在完成上述EDA任务后,我们发现了一些需要在数据清理阶段解决的问题。
- 在年龄、舱位和登船栏中有一些数据丢失。
- 在那些数据缺失的栏目中,年龄是数字,而机舱和登船是离散数据。
- 年龄和登船的缺失值很少,而船舱有大量的缺失值。
接下来进行数据清洗。有很多方法可以修复数据缺口,例如,
- 如果有任何缺失,就删除整个行。
- 按原样留下(对于某些类型的机器学习算法,NULL值会导致问题。 所以,这个选项将不适用)。
- 用平均值填补空白(只适用于数字变量)。
- 用模式值填补空白(对数字变量和分类变量都适用)。
- 定制的空白填补算法(可以非常复杂,比如使用另一个机器学习模型来预测缺失值)
在这里,让我们采取相对简单的方法。也就是说,用平均值来填充数字列,然后用模式来填充分类值。
特征工程是训练机器学习模型的一个非常重要的步骤,特别是对于经典的机器学习算法。有时它占据整个工作流程的大部分时间,因为我们可能需要多次进行这个阶段以提高我们的模型的性能。在我们的数据集中,首先我们需要识别一些不能使用或没有用的特征。PassengerId特征需要被拒绝,因为它没有用。Name特征也应该被拒绝,因为它对乘客是否生存没有任何影响。Cabin特征可以被拒绝,因为有超过70%的缺失。Ticket特征也应该被拒绝,因为它在EDA中没有显示任何模式。我们选择其余的特征,它们对分类模型很有用。因为我们要使用决策树,所以如果有任何对模型没有帮助的特征,它们就不太可能被选为树的分割节点。 让算法告诉我们。因此,让我们建立我们的特征数据框和标签系列。
1. features = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']
2. label = 'Survived'
3. df_train_features = df_train[features]
4. s_train_label = df_train[label]
现在我们可以使用这些特征来训练我们的模型。 然而,由于我们要使用Sci-kit Learn库,而它的决策树算法不接受字符串类型的分类值,我们必须对我们的特征数据集进行独热编码(One Hot Encoding)。具体来说,我们的Sex和Embarked特征是字符串类型的,需要转换为数字。我们得到了一个891 x 5的矩阵,这意味着编码的特征集有5列。这是因为性别特征有两个不同的值:女性和男性。而Embarked特征有3个不同的值: S、C和Q。通过独热编码将两个特征合为一个特征。现在,我们可以训练我们的决策树模型。
1. **from** sklearn.tree **import** DecisionTreeClassifier
2. model = DecisionTreeClassifier()
3. model.fit(df_train_features, s_train_label)
训练完成后,我们的模型是什么样子的?对于大多数机器学习算法来说,要想知道模型的样子并不容易。然而,我们可以直观地看到决策树的模型,看看节点是如何分割的。图10-9展示了决策树模型的可视化子树。每一个树节点里面的第一行代表子树划分标准,第二行gini代表基尼系数,第三行samples代表子树样本总数,第四行value代表每个类别样本的数量。基尼分数是量化节点纯度的度量,类似于熵。基尼系数大于零意味着该节点中包含的样本属于不同的类。叶子的基尼分数为零,这意味着每个叶子中的样本属于一个类。当纯度较高时节点/叶子的颜色较深。
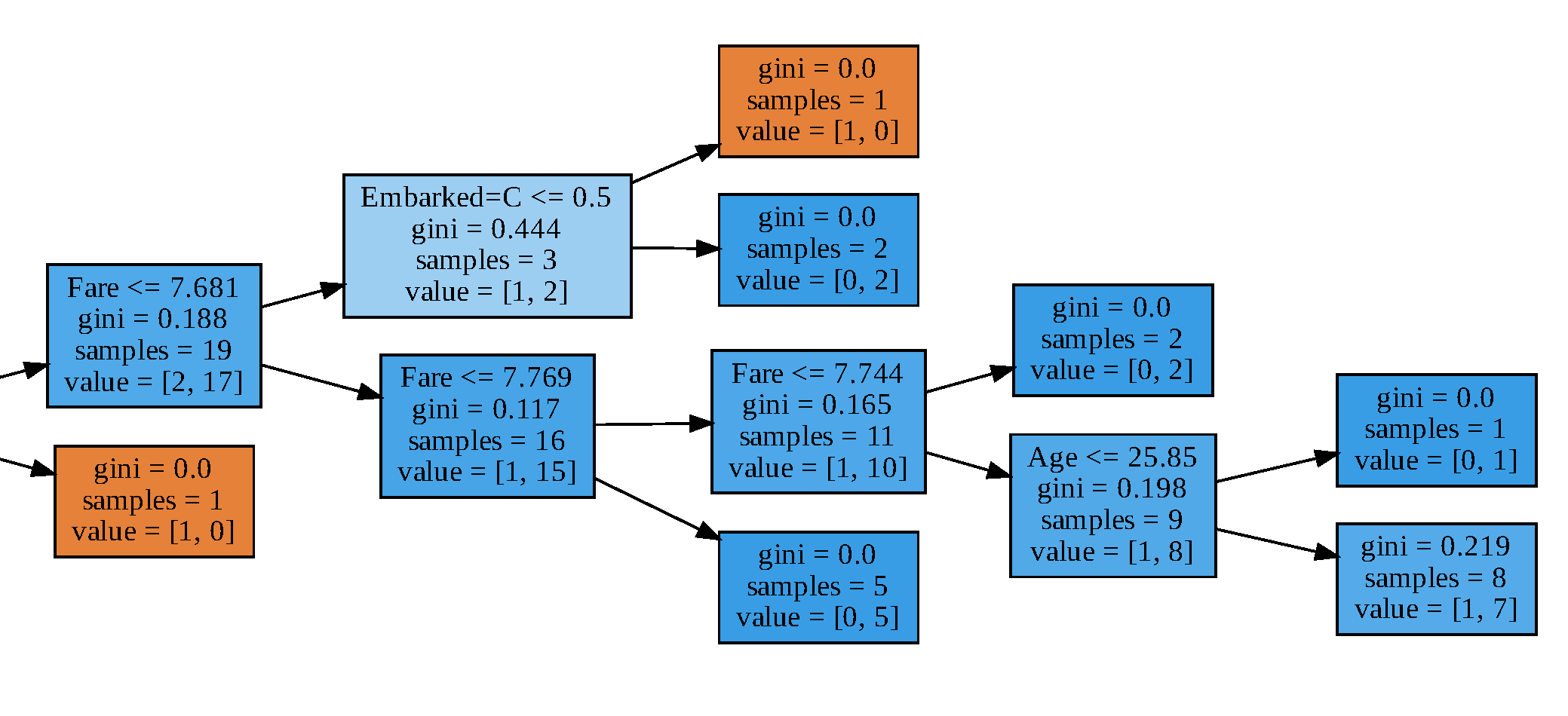
决策树模型子树
在最后阶段,我们需要评估我们的模型。在实践中,我们通常需要将我们的原始数据集分成训练和测试数据集。本节,我们用交叉验证法来评估我们的模型
交叉验证的基本思想是评估模型的训练方法和超参数,而不是评估一个训练好的模型。它遵从以下步骤。
(1)将数据集分成n个大小相等的片段。
(2)使用n-1个片段训练模型,其余1个片段将被用作测试集。
(3)计算模型的预测精度。
(4)重复步骤2-3,使用不同的片段作为测试集,直到所有的片段都被评估。
(5)得到n个准确率的平均值,这将被视为模型的得分。
我们通过代码实现,最终我们得到了78.01%的分类准确率。
1. **import** numpy as np
2. **from** sklearn.model_selection **import** cross_val_score
3. accuracy_list = cross_val_score(model, df_train_features, s_train_label, cv=10)
4. **print**(f'The average accuracy is {(np.mean(accuracy_list)*100).round(2)}%')
