机器学习问题要处理大量的数据，并在很大程度上取决于用于训练模型的算法。根据实际的问题，有各种方法和算法来训练一个机器学习模型。监督学习和无监督学习是这些方法中最突出的两种。

在现实生活中，向特定目标受众推销产品或服务是一个重要问题。这种问题可以在一种无监督学习的帮助下轻松解决，这种学习被称为聚类。在本节中，我们将结合现实生活中的问题和例子来解释聚类算法。让我们首先了解什么是无监督学习和聚类。

无监督学习是机器学习中处理无标签数据的领域。广义上讲，它涉及根据一些共享属性对数据集进行分割，并检测数据集中的异常情况。它通过聚合具有类似属性的变量来简化数据集。主要目标是研究数据集中的基本结构。无监督学习所解决的最常见的两类问题是聚类和降维。在这篇文章中，我们将重点讨论机器学习中的聚类算法。

集群这个词来自一个古老的英语单词“clyster”，意思是一堆。 集群是指定位或发生在一起的类似事物或人的团体。 通常，一个集群中的所有点都描绘了类似的特征，因此可以用机器学习来识别性状并隔离这些集群。这使得机器学习的许多应用成为解决各行业数据问题的基础。

聚类算法将数据点划分为多个相似值的聚类。换句话说，聚类的目的是将具有相似性状的群体分离出来，并将它们捆绑在一起，形成不同的集群。理想情况下，它是在机器中实现人类的认知能力，使它们能够识别不同的物体，并根据它们的自然属性对其进行区分。 与人类不同，除非在一个巨大的相关数据集上进行适当的训练，否则机器很难从苹果或橙子中识别出来。这种训练是通过无监督的学习算法，特别是聚类来实现的。

K-Means聚类

K-Means是迄今为止最流行的聚类算法，因为它非常容易理解，并适用于广泛的数据科学和机器学习问题。下面是你如何将K-Means算法应用于你的聚类问题。

1. 随机分配k中心点。
2. 根据这些中心点（以及观测值与中心点的距离），将每个观测值分配到一个聚类。
3. 计算每个聚类的平均坐标。 这些是我们的新中心点。
4. 根据新的中心点重新分配聚类。
5. 继续重复步骤3和4，直到收敛。

为了使编码更容易，让我们定义几个辅助函数。首先让我们写一个计算2个点之间的欧几里得距离。

1. **def** calc_distance(X1, X2):
2. **return** (sum((X1 - X2)**2))**0.5

接下来，我们需要一个函数，给定一组中心点，可以告诉我们每个观测值属于哪个聚类。下面的函数使用嵌套的for循环来计算每个观察值和每个中心点之间的距离。 然后，它根据观察结果最接近的中心点将其分配到一个聚类。输出是每个观测值的聚类标签的列表。

1. # 根据最近的中心点分配聚类
2. **def** assign_clusters(centroids, cluster_array):
3. clusters = []
4. **for** i **in** range(cluster_array.shape[0]):
5. distances = []
6. **for** centroid **in** centroids:
7. distances.append(calc_distance(centroid, cluster_array[i]))
8. cluster = [z **for** z, val **in** enumerate(distances) **if** val==min(distances)]
9. clusters.append(cluster[0])
10. **return** clusters

现在我们需要一个用于更新步骤的函数，在这个步骤中我们分配新的中心点。下面的函数将数据（每个观测值的票价和年龄）和其所属的当前聚类、聚类一起串联到一个数据帧。然后我们可以通过聚类过滤数据帧，只得到属于某个特定聚类的观测值，并计算这些观测值的平均值。这些计算出的平均值就是我们的新中心点。

1. # 根据每个聚类的平均值计算新的中心点
2. **def** calc_centroids(clusters, cluster_array):
3. new_centroids = []
4. cluster_df = pd.concat([pd.DataFrame(cluster_array),
5. pd.DataFrame(clusters,
6. columns=['cluster'])],
7. axis=1)
8. **for** c **in** set(cluster_df['cluster']):
9. current_cluster = cluster_df[cluster_df['cluster']\
10. ==c][cluster_df.columns[:-1]]
11. cluster_mean = current_cluster.mean(axis=0)
12. new_centroids.append(cluster_mean)
13. **return** new_centroids

现在我们可以开始运行K-Means聚类算法了。接着使用上一节中的泰坦尼克号数据集展示K-Means聚类算法是怎么进行聚类的。由于我们的主要重点是建立K-Means并探索它是如何工作的，我们将只用数据集中的两列来工作：票价（买票的价格）和乘客的年龄。按票价和年龄对数据进行排序，因为我最终将挑选前k个观测值作为聚类中心。排序确保了我将挑选k个彼此都非常相似的观测值作为我的初始中心点。这样一来，开始的中心点将是次优的，我们可以更清楚地看到算法是如何收敛到更好的中心点的。

我们聚类4个集群。就像我之前说的，我们会有目的地选择不好的起始中心点，这样我们就可以看到算法所做的改进。根据它最接近的中心点，将每个观测值分配到一个聚类。实际中我们不必这样做，因为这样会减慢速度。

我们运行20次迭代，我们反复计算新的中心点和新的集群，这样我们就能得到最佳的集群。回顾一下，通过重复这个计算集群平均值的过程，并根据这些新的中心点分配新的聚类，这是算法收敛到最终聚类的方式。图10-10展示了迭代过程图，可以看到在迭代到第六次的时候，K-Means算法就基本收敛。

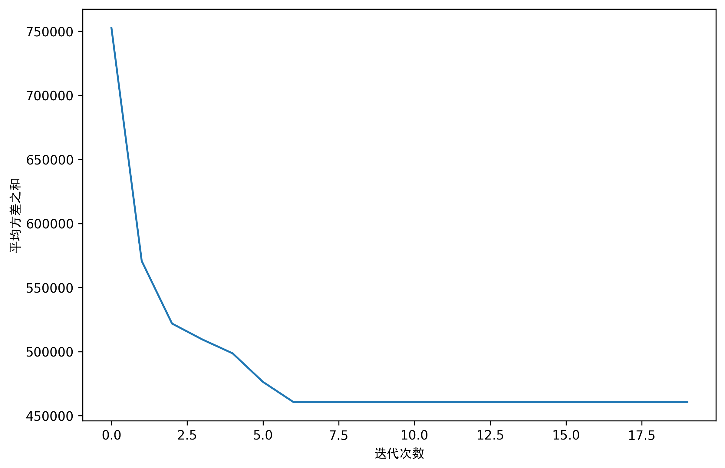
K-Means迭代图

让我们来看看我们的集群是否变得更好。 回顾一下，我们从任意选择的中心点开始。 下面是基于这些初始中心点的集群（每种颜色是一个集群）。 似乎有一些基于年龄的分离，但效果不显著。

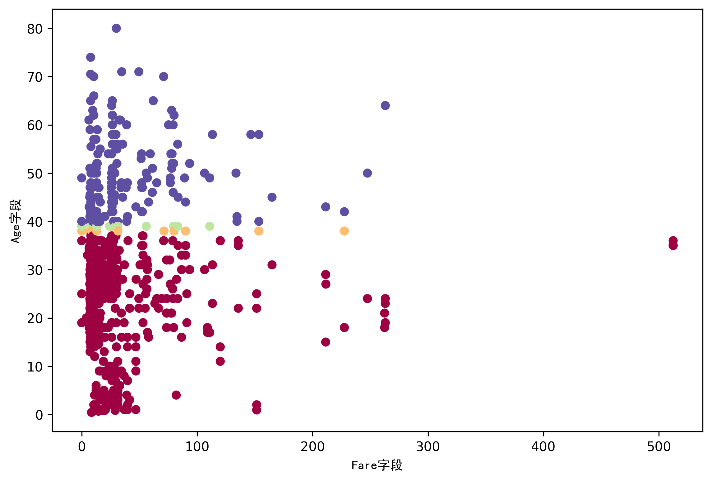
初始聚类图

现在，这里是聚合的集群。这些群组似乎更有意义地进行了区分。

1. 年长的低票价的人（绿色）。
2. 年轻的低票价的人（深红色）。
3. 那些能买得起高级票的人（蓝色）。
4. 而那些能买得起超级昂贵门票的人（黄金）。

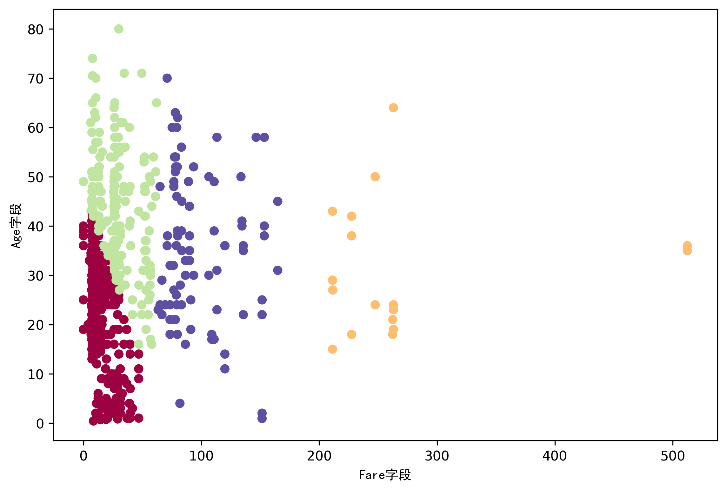
迭代收敛聚类图

我们可以检查我们做得如何的另一个方法是，看我们的集群的生存概率是否不同。 k-means聚类是无监督的。所以我们没有明确地训练模型来预测乘客是否存活。相反，我们希望通过产生有意义的差异化集群，我们可以找到那些在我们关心的事情上，也恰好表现不同的群体。而且，相对于我们最初的集群，我们收敛的集群似乎在预测生存方面做得更好。

显然，我们还有很多事情可以做，包括增加更多的特征，而不是只有2个。调整集群的数量，并试图更好地了解每个集群的关键特征。读者可通过提供的源代码自行尝试不同特征的聚类方案。

密度聚类

基于密度的有噪声的空间聚类应用（DBSCAN）是一种流行的无监督学习方法，应用于模型建立和机器学习算法中。

DBSCAN将高密度的群组与低密度的群组分开。鉴于DBSCAN是一种基于密度的聚类算法，它能很好地寻找数据中观察值密度高的区域。DBSCAN也可以将数据分类为不同形状的聚类，这是另一个强大的优势。DBSCAN是这样工作的。

1. 将数据集分成k个维度。
2. 对于数据集中的每一个点，DBSCAN在该数据点周围形成一个k个维度的形状，然后计算有多少数据点落在这个形状内。
3. DBSCAN将这个形状算作一个簇。 DBSCAN通过遍历集群内的每一个单独的点，并计算附近其他数据点的数量，迭代式地扩大集群。

DBSCAN将首先把数据分为k个维度。在DBSCAN完成后，它将从一个随机的点开始，计算附近有多少其他的点。DBSCAN将继续这个过程，直到附近没有其他数据点，然后寻找形成第二个集群。在DBSCAN工作之前，我们需要给它一些参数。DBSCAN算法需要2个基本参数。

eps: 指明各点之间的距离有多大，才能被认为是集群的一部分。这意味着，如果两点之间的距离低于或等于这个值（eps），这些点就被视为邻居。

minPoints: 形成一个密集区域的最小点数。例如，如果我们将minPoints参数设置为5，那么我们至少需要5个点才能形成一个密集区域。

参数估计是每个数据挖掘任务的一个问题。为了选择好的参数，我们需要了解它们是如何被使用的，并且至少要对将要使用的数据集有一个基本的前期了解。参数的选取至关重要。如果选择的eps值太小，很大一部分数据将不会被聚类。它将被视为异常值，因为不满足创建密集区域的点的数量。另一方面，如果选择的数值太高，集群就会合并，大多数物体会在同一个集群中。eps应该根据数据集的距离来选择，但一般来说，小的eps值是比较好的。一般来说，最小点数minPoints可以从数据集的维数D中得到，因为minPoints ≥ D + 1。对于有噪音的数据集来说，较大的数值通常更好，而且会形成更多的重要聚类。minPoints的最小值必须是3，但数据集越大，应该选择的minPoints值就越大。

DBSCAN的优势是在一个给定的数据集中，它非常善于分离高密度和低密度的集群。并且在处理数据集中的异常值方面非常出色。DBSCAN的劣势也很突出，虽然DBSCAN在分离高密度集群和低密度集群方面非常出色，但DBSCAN在处理密度相近的集群时却很困难。DBSCAN无法有效的运作在高维数据中。如果给定的数据维度太多，DBSCAN就会受到影响。

我们同样使用之前的泰坦尼克号的生存数据集来展示密度聚类的运行。同样的，在运行DBSCAN之前，我们需要进行数据清洗。和之前不同的是，我们需要对数值进行标准化处理。对数值进行归一化是很重要的，因为它使我们更容易找到一个合适的邻域半径（eps）的距离。

我们选取Age和Fare字段进行聚类。

1. **from** sklearn.cluster **import** DBSCAN
2. DBSC = DBSCAN(eps=15, min_samples=5)
3. x = titanic[['Fare','Age']].copy(deep=True)
4. x['Age'] = x['Age'].fillna(x['Age'].mean())
5. cluster_D = DBSC.fit_predict(x)

我们来可视化DBSCAN的聚类效果。

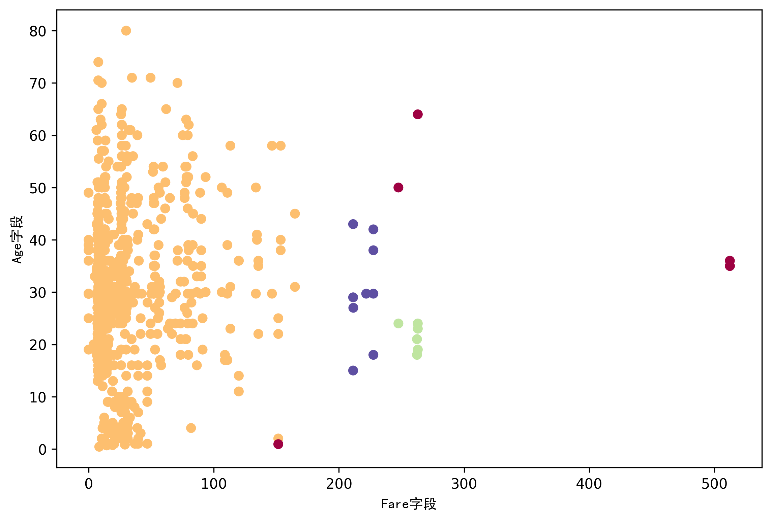
DBSCAN聚类图

这个样本数据集中的DBSCAN聚类没有形成任何的形状，甚至在边缘形成类似圆环的集群。相比于K-Means算法和层次聚类算法，DBSCAN在检测异常值方面表现得非常好。例如图10-12中深红色的点就可视为异常点。DBSCAN非常适合与异常值的检测，可以在数据预处理过程中运用DBSCAN来进行异常值处理。读者可尝试去掉DBSCAN中的低密度类别样本后进行K-Means聚类，观察前后的变化。

层次聚类

层次聚类（HC）是聚类分析的一种方法，用于将类似的数据点聚在一起。层次聚类遵循自上而下或自下而上的聚类方法。分别对应两种类型的分层聚类方法：分离式聚类、聚合式聚类。

层次分离聚类（HDC）是一种自上而下的聚类方法，最初，数据集中的所有点都属于一个聚类，分裂是随着层次的下移而递归进行的。分离式聚类遵从以下步骤：

1. 最初，数据集中的所有点都属于一个单一的集群。
2. 将集群划分为两个最不相似的集群。
3. 递归地形成新的集群，直到获得所需的集群数量。

在选择要分裂的集群时，检查每个集群的平方误差之和（SSE），并选择数值最大的一个。具有最大SSE值的集群被分离成2个集群，从而形成一个新的集群。决定分割哪个集群后，那么如何将所选的集群分割成两个集群。一种常见方法是使用沃德法（Ward’s method）来追求拆分后SSE达到最小。由于离群点或噪音的存在，可能会导致形成边缘的新集群。为了处理数据集中的噪音，使用一个阈值来确定终止标准，即不要产生太小的集群。

层次聚合聚类（HAC）是一种自下而上的方法。最初，每个数据点都是自己的一个聚类，随着层次的提升，进一步合并成大的聚类。聚合式聚类遵从以下步骤：

1. 最初，所有的数据点都是它自己的一个集群。
2. 取两个最近的聚类，并将它们连接起来，形成一个单一的聚类。
3. 递归地进行第2步，直到得到所需的集群数量。

为了获得所需的聚类数量，需要将聚类的数量从最初的n个聚类（n等于数据点的总数）聚合。通过计算两个聚类之间的相似度，将两个聚类合并。有一些方法被用来计算两个集群之间的相似度。

1. 两个聚类中最接近的两个点之间的距离。
2. 两个聚类中最远的两个点之间的距离。
3. 两个聚类中所有点的平均距离。
4. 两个聚类的中心点之间的距离。

让我们来看看一个具体的例子，看看我们如何使用聚合层次聚类来标记数据。继续使用泰坦尼克号的生存数据集，我们之前已经得到了清洗干净的原始数据，直接使用层次聚类算法：

1. **from** sklearn.cluster **import** AgglomerativeClustering
2. model = AgglomerativeClustering(n_clusters=4)
3. x = titanic[['Fare','Age']].copy(deep=True)
4. x['Age'] = x['Age'].fillna(x['Age'].mean())
5. cluster_D = model.fit_predict(x)

树状图给出了所走路径的全貌，从所有单独的点（图的底部）移动到一个单一的集群（图的顶部）。我们可以用树状图来直观地显示聚类的历史，并找出最佳的聚类数量。确定不与其他任何群组相交的最大垂直距离。在两端画一条水平线，最佳集群数等于穿过水平线的垂直线数。层次聚类的树状图如图10-13，可以观察到最佳集群数为3，这里为了更好的与之前的K-Means算法和DBSCAN算法作比较，我们选取4作为聚类的集群数。

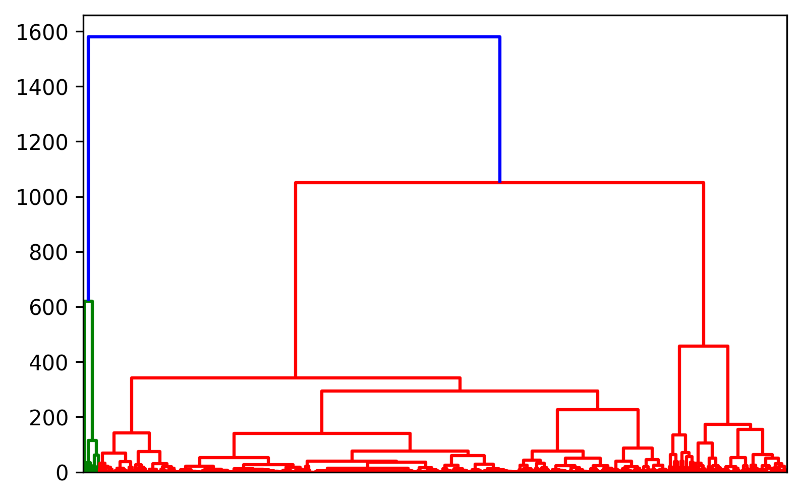
层次聚类树状图

我们使用欧氏距离作为点与点之间距离的度量，并使用沃德法来计算聚类的接近程度。最终我们可以得到4个层次聚类的集群。

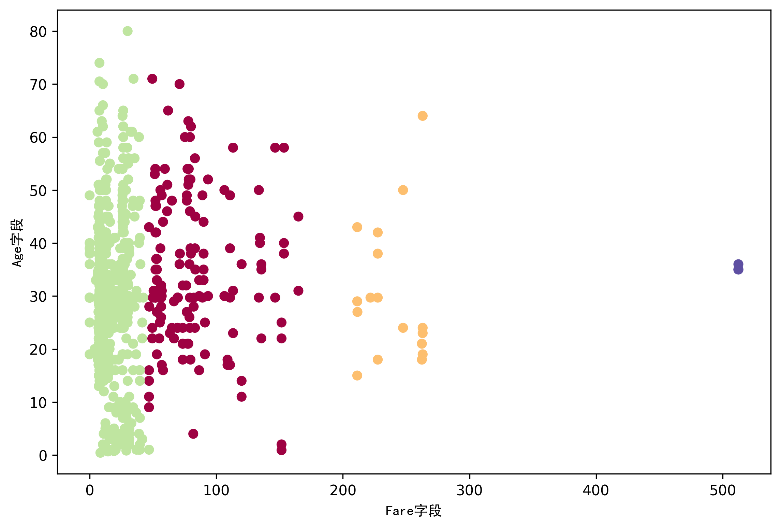
层次聚类图

使用层次聚合聚类的优点是分析树状图的能力，它提供了对任何两个数据点之间的相似性有直观的展示。一般来说，可以用层次聚合聚类和K-Means生成非常相似的聚类，但由于能够看到每个数据点的路径，使得层次聚合聚类在分析单个数据点或聚类之间的相似性和差异时更加有用。但分层聚类有一些缺点，由于空间和时间上的复杂性，这些算法不适合运行与大型的数据集。

代码

聚类