数据分析与挖掘(一)回归模型实战
Published:
回归分析在维基百科中被定义为:
在统计建模中,回归分析是一套用于估计因变量(通常称为“结果变量”)和一个或多个自变量(通常称为“预测因素”、“协变量”或“特征”)之间关系的统计过程。
你经常会听到与回归分析有关的术语是:
(1)因变量或目标变量:要预测的变量。
(2)独立变量或预测变量:用于估计因变量的变量。
(3)离群点:与其他观测值有显著差异的观测值。应该避免这种情况,因为它可能会妨碍结果。
(4)多重共线性:两个或多个自变量高度线性相关的情况。
(5)同质性或方差的同质性:误差项在自变量的所有数值中都是相同的情况。
回归分析主要用于两个不同的目的。首先,它被广泛用于预测和预报,这与机器学习领域相重叠。其次,它也被用来推断自变量和因变量之间的因果关系。
在数据科学和机器学习中,有各种类型的回归方法被广泛的使用。每种类型在不同的情况下都有自己的重要性,但核心是所有的回归方法都是分析自变量对因变量的影响。这一节我们将回归分析方法简单的分为线性回归和非线性回归,我们将从实际案例中学习到经典的回归模型。
线性回归
回归分析中最常见的模型是线性回归。这种模型通过拟合一个线性方程找到自变量和因变量之间的关系。拟合这种回归线最常用的方法是使用最小二乘法,计算出最佳拟合线,使每个数据点到线的垂直偏差的平方之和最小。
建立一个线性回归模型只是工作的一半。为了在实践中真正可用,该模型应符合线性回归的假设:
(1)参数是线性的。
(2)样本能代表整个数据。
(3)自变量的测量是没有误差的。
(4)观察值的数量必须大于自变量的数量。
(5)独立变量内部没有多重共线性。
要满足所有这些假设是很难的,所以实践者们开发了各种方法,以在现实世界的环境中保持部分或所有这些理想的特性。
为了展示之前介绍的一些概念,我们在波士顿住房数据集上实现了一个线性回归模型。下面是代码,以及对每个模块的简要解释。我们将采用房屋数据集,其中包含波士顿不同房屋的信息。这个数据最初是UCI机器学习资源库的一部分,现在已经被删除了。我们也可以从scikit-learn库中获取这些数据。在这个数据集中有506个样本和13个特征变量。我们的目标是使用给定的特征来预测房屋的价格价值。
首先我们从库中加载加州房屋数据,数据集中有以下字段:
CRIM: 各镇的人均犯罪率
ZN: 划分为25,000平方英尺以上的住宅用地的比例
INDUS: 每个镇的非零售商业亩数比例
CHAS: 查尔斯河虚拟变量(=1,如果区块与河流相邻;否则为0)。
NOX: 一氧化氮浓度(每1000万份)。
RM: 每个住宅的平均房间数
AGE: 1940年以前建造的业主自用单元的比例
DIS: 到波士顿五个就业中心的加权距离
RAD: 辐射状高速公路的可达性指数
TAX: 每10,000美元的全值财产税率
PTRATIO: 各镇的学生-教师比率
B: 1000(Bk-0.63)²,其中Bk是各镇[非裔美国人]的比例
LSTAT: 人口中地位较低者的比例
MEDV: 业主自用房屋的中值,单位为1000美元
房屋的价格由变量MEDV表示,它定义了我们的因变量。其余的是自变量,我们将在此基础上预测房屋的价值。让我们首先绘制目标变量MEDV根据AGE和CRIM的分布。这张图是绘制美国波士顿的情况。正如所观察到的,年龄大的房子比其他地方的要便宜,地区犯罪率高的房子比其他地方的要便宜。
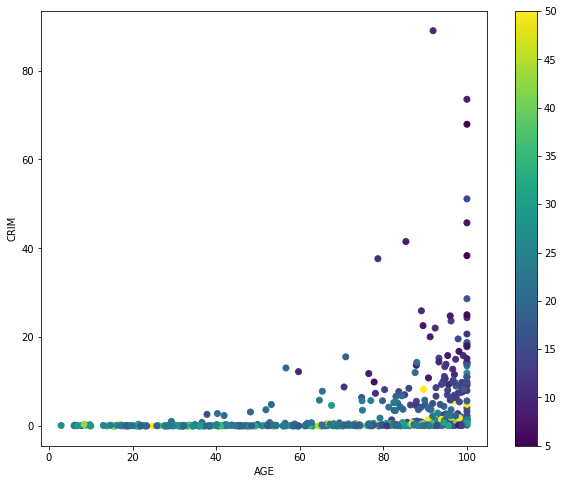
年龄和犯罪率影响下的波士顿房价
我们创建一个相关矩阵来衡量变量之间的线性关系。相关矩阵可以通过使用pandas数据框架库的corr函数来形成。如图10-2所示,我们将使用seaborn库的heatmap函数来绘制相关矩阵。
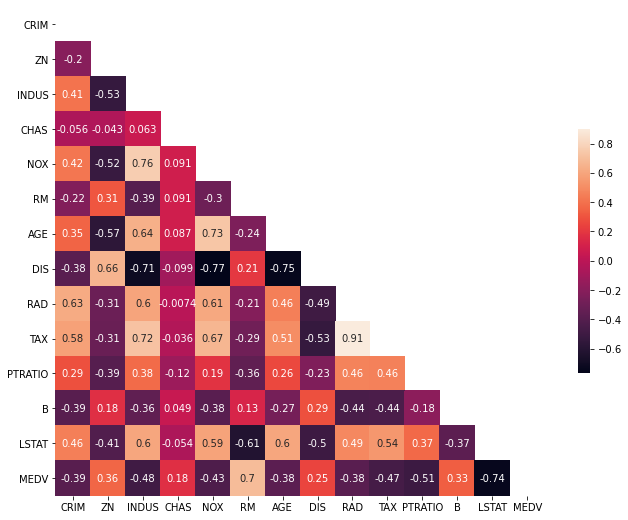
自变量的相关矩阵
相关系数的范围是-1到1。如果数值接近1,意味着两个变量之间有很强的正相关关系。当它接近于-1时,这两个变量有很强的负相关关系。为了更好的拟合回归模型,我们选择那些与我们的目标变量MEDV有高度相关性的特征。通过查看相关矩阵,我们可以看到RM与MEDV有很强的正相关(0.7),而LSTAT与MEDV有很高的负相关(-0.74)。
在为线性回归模型选择特征时,重要的一点是要检查多重共线性。特征RAD、TAX的相关度为0.91。这些特征对彼此之间有很强的关联性。这里为了更好的可视化,我们选择相关性最强的LSTAT变量来对房价进行拟合。图10-3中可以观察到价格往往随着LSTAT的增加而下降。尽管它看起来并不完全是沿着一条线性直线。
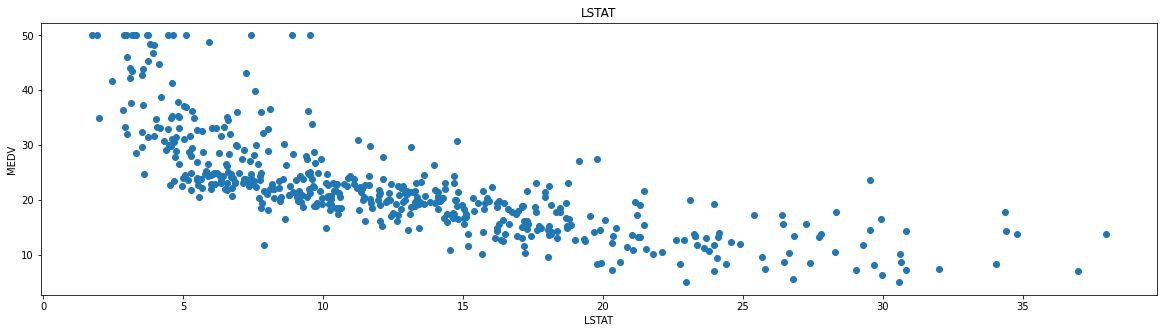
LSTAT数据分布图
接下来,我们把数据分成训练集和测试集。我们用80%的样本训练模型,用剩下的20%测试。我们这样做是为了评估模型在未见过的数据上的表现。线性回归试图学得函数
$f(x_i) = ωx_i + b.$
使得预测值与实际值越接近越好。平方误差是回归任务中最常用的性能度量,我们最小化平方误差使得线性函数更好的拟合训练数据,即
$arg\operatorname{}{\sum_{i = 1}^{m}{(f\left( x_{i} \right) - y_{i})}^{2}.}$
基于平方误差最小化的方法称为“最小二乘法”。在线性回归中,最小二乘法试图找到一条直线或超平面,使得样本到直线或超平面的欧式距离之和最小。在训练集上训练线性回归模型,代码如下。
1. **from** sklearn.linear_model **import** LinearRegression
2. **from** sklearn.metrics **import** r2_score, mean_squared_error
3. lin_model = LinearRegression()
4. lin_model.fit(X_train, Y_train)
5. # model evaluation for testing set
6. y_test_predict = lin_model.predict(X_test)
7. rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
8. r2 = r2_score(Y_test, y_test_predict)
在测试集上面使用RMSE和R2-score验证我们的模型的拟合程度。我们得到RMSE的值为6.20,R2-score的值为0.50。如图10-3所示,LSTAT的测试数据被一条直线所拟合,数据到直线的垂直距离之和达到最小值。当然在实际应用中,只用一个自变量是无法很好的拟合目标模型的。通常会使用多个特征来进行线性回归,并学习到一个特征空间的超平面来拟合回归模型。
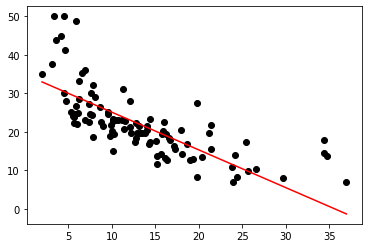
LSTAT测试数据线性拟合图
逻辑回归
在此之前,我们都假设预测变量和被预测变量之间为线性关系,但是在某些情况下,非线性函数形式可能更加符合真实情况。虽然此时为非线性函数形式,但是模型中的参数认为线性的。最常见的变换方式是对变量做自然对数变换,这就是逻辑回归。
逻辑回归是非线性回归中的一种,将逻辑回归作为一个二分类器能解决一些分类问题。Logistic回归是一种分类算法,用于将观察结果分配到一组离散的类别中。一些分类问题的例子有:垃圾邮件或不是垃圾邮件,网上交易欺诈或不是欺诈,肿瘤恶性或良性。Logistic回归使用logistic sigmoid函数对其输出进行转换,以返回一个概率值。那么为什么使用逻辑回归而不是线性回归呢,这里给出一个例子。假设我们有关于肿瘤大小与恶性程度的数据。由于这是一个分类问题,所有的值都位于0和1之间。如果我们拟合最佳回归线,假设阈值为0.5,我们可以得到一个合理的回归线。我们可以在X轴上确定一个点,从这个点开始,所有位于其左侧的数值都被认为是一个负类,所有位于其右侧的数值都是正类。但是,如果数据中存在一个异常点回归将会变得困难。我们拟合最佳回归线,它仍然不足以决定任何点的类别。它将会把一些阳性类的例子放到阴性类中。因此,仅仅一个离群点就干扰了整个线性回归的预测。这就是逻辑回归发挥作用的地方。
逻辑回归的假设将损失函数限制在0和1之间。因此,线性函数不能代表它,因为它的值可能大于1或小于0,而根据逻辑回归的假设,这是不可能的。为了将预测值映射到概率,我们使用Sigmoid函数。该函数将任何实值映射为0和1之间的另一个值。在机器学习中,我们使用Sigmoid来将预测值映射为概率。Sigmoid函数为
$f\left( x \right) = \frac{1}{1 + e^{- (x)}}$
逻辑回归是一种Sigmoid函数,它将线性回归的值转化为一个接近0或1的值。将线性回归函数代入Sigmoid函数得到
$f\left( x \right) = \frac{1}{1 + e^{- (\omega^{T}x + b)}}$
正如在线性回归中,我们需要一种方法来估计参数。因此,我们使用“最大似然函数”来估计参数ω和b。对似然函数取对数可得
$\mathcal{l}\left( \omega,b \right) = \sum_{i = 1}^{m}{\ln{p(y|x,\omega,b)}}$
与线性回归类似,我们使用p值来确定是否拒绝零假设。Z-统计学也被广泛使用。 一个大数Z统计量意味着拒绝零假设。零假设是指,特征和目标之间没有关联性。
当我们将输入通过预测函数并返回0和1之间的概率分数时,我们希望我们的分类器能根据概率给我们一组输出或类别。逻辑回归模型应符合以下假设:
(1)二元逻辑回归要求因变量是二元的
(2)因变量的因子水平1应该代表预期的结果。
(3)自变量应该是相互独立的。也就是说,模型应该有很少或没有多重共线性。
(4)自变量与对数几率呈线性关系。
(5)逻辑回归需要相当大的样本量。
接下来通过实际案例来更好的理解逻辑回归的奥秘。实验数据集来自UCI机器学习资源库,它与一家葡萄牙银行机构的电话营销活动有关。其分类目标是预测客户是否会认购定期存款(变量y)。该数据集提供了银行客户的信息。它包括41,188条记录和21个字段。
age: 年龄(数值型)。
job: 工作类型(分类:”行政”、”蓝领”、”企业家”、”女佣”、”管理”、”退休”、”创业”、”服务”、”学生”、”技术员”、”失业”、”未知”)。
marital: 婚姻状况(分类:”离婚”、”已婚”、”单身”、”未知”)。
education: 教育程度”基础4年”、”基础6年”、”基础9年”、”高中”、”文盲”、”专业课程”、”大学学位”、”未知”。
default: 是否有违约的信贷?(分类:”没有”、”有”、”未知”)。
housing: 是否有住房贷款?(分类: “没有”, “有”, “未知”)。
loan: 有个人贷款吗?(分类: “没有”, “有”, “未知”)。
contact: 联系通信类型(分类:”手机”、”电话”)。
month: 最后一次联系的年份的月份(分类:”1”, “2”, “3”, …, “11”, “12”)。
day_of_week: 最后一次联系的星期(分类:”周一”, “周二”, “周三”, “周四”, “周五”)。
duration: 最后一次接触的时间,以秒为单位(数字)。
pdays: 客户在上次活动中被联系后的天数(数字,999表示客户没有被联系过)。
previous: 在这次活动之前,为这个客户进行的接触次数(数值型)。
poutcome: 上一次营销活动的结果(分类:”失败”、”不存在”、”成功”)。
emp.var.rate: 就业变化率。
cons.price.idx: 消费者价格指数。
cons.conf.idx: 消费者信心指数。
euribor3m: 欧洲银行3个月利率。
nr.employed: 雇员人数。
设计预测变量为客户是否认购了定期存款。(”1”表示 “是”,”0 “表示 “否”)数据集的education字段有很多类别的数据,我们需要减少类别,以便更好地进行建模。 对预测变量进行分析可得出订阅分布是不平衡的,无订阅和订阅客户的比例是89:11。 在我们继续平衡各类数据之前,让我们再做一些探索。
| y | age | duration | campaign | pdays | previous | emp_var_rate | cons_price_idx |
|---|---|---|---|---|---|---|---|
| 0 | 39.91 | 220.84 | 2.63 | 984.11 | 0.13 | 0.24 | 93.6 |
| 1 | 40.91 | 553.19 | 2.05 | 792.03 | 0.49 | -1.23 | 93.35 |
观察到,购买定期存款的客户的平均年龄高于没有购买的客户。对于购买的客户来说,pdays(自最后一次联系客户以来的天数)较低,这是可以理解的。pdays越低,对最后一次通话的存量就越好,因此销售的机会就越大。令人惊讶的是,购买了定期存款的客户的活动(在当前活动期间进行的接触或呼叫的数量)较少。我们可以计算其他分类变量的分类平均数,如教育和婚姻状况,以便更详细地了解我们的数据。
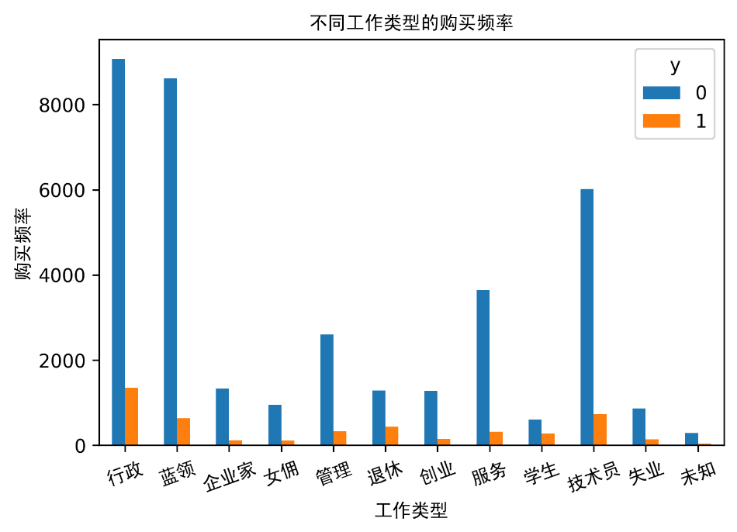
不同工作类型的购买频率
购买押金的频率在很大程度上取决于工作职位。 因此,职称可以成为预测变量的一个很好的预测因素。通过更多的统计发现,婚姻状况似乎不是预测变量的一个强有力的预测因素。教育程度似乎是预测变量的一个很好的预测因素。在这个数据集中,大多数银行客户的年龄在30-40岁之间。
统计分析结束后,根据观察得到的结果使用SMOTE进行过度采样,用于解决类别不平衡问题。有了我们的训练数据,我将使用SMOTE算法对无订阅客户进行上采样。 在高层次上,SMOTE通过从小类(无订阅)中创建合成样本而不是创建副本来工作。随机选择k-近邻中的一个样本,并使用它来创建一个类似的但随机调整的新样本。最终达到样本类别的平衡,实现代码如下
1. X = data_final.loc[:, data_final.columns != 'y']
2. y = data_final.loc[:, data_final.columns == 'y']
3. **from** imblearn.over_sampling **import** SMOTE
4. os = SMOTE(random_state=0)
5. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
6. columns = X_train.columns
7. os_data_X,os_data_y=os.fit_sample(X_train, y_train)
8. os_data_X = pd.DataFrame(data=os_data_X,columns=columns )
9. os_data_y= pd.DataFrame(data=os_data_y,columns=['y'])
现在我们有了一个完美的平衡数据! 你可能已经注意到,我们只对训练数据进行了过度采样,因为只对训练数据进行过度采样,测试数据中的任何信息都不会被用来创建合成观测值。因此,没有任何信息会从测试数据中渗入模型训练。接着我们进行递归特征消除(RFE)。RFE是基于反复构建模型并选择表现最好或最差的特征的想法,将该特征放在一边,然后用其余的特征重复这一过程。 这个过程一直应用到数据集中的所有特征都用完为止。RFE的目标是通过递归地考虑越来越小的特征集来选择特征。除了我们选取的四个变量外,大多数变量的p值都小于0.05,因此,我们将把它们删除。
选择好特征之后,就可以开始构建模型了。逻辑回归模型的代码如下
1. **from** sklearn.linear_model **import** LogisticRegression
2. **from** sklearn **import** metrics
3. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
4. logreg = LogisticRegression()
5. logreg.fit(X_train, y_train)
预测测试集结果并计算准确性,逻辑回归分类器在测试集上的准确性为0.74。为了更直白的体现模型的好坏,我们使用计算精度、召回率、F值和支持率来评价模型。
定义TP是真阳性的数量,FP是假阳性的数量,TN是真阴性的数量,FN是假阴性的数量。
精确度是$\frac{\text{TP}}{TP + FP}$。直观地说,精度是指分类器在样本为阴性时不将其标记为阳性的能力。
召回率是$\frac{\text{TP}}{TP + FN}$。召回率直观地说就是分类器在阳性样本中找到所有阳性样本的能力。
F值可以被解释为精确度和召回率的加权平均值,其中F值在1时达到最佳值,在0时达到最差值。F1值意味着召回率和精确度同等重要。
支持量是测试集中每个类的出现次数。
| 精度 | 召回率 | F1值 | 支持量 | |
|---|---|---|---|---|
| 0 | 0.71 | 0.8 | 0.75 | 7666 |
| 1 | 0.77 | 0.67 | 0.72 | 7675 |
| 平均/总和 | 0.74 | 0.74 | 0.74 | 15341 |
在整个测试集中,74%的促销定期存款是客户喜欢的。 在整个测试集中,74%的客户首选被推荐定期存款。
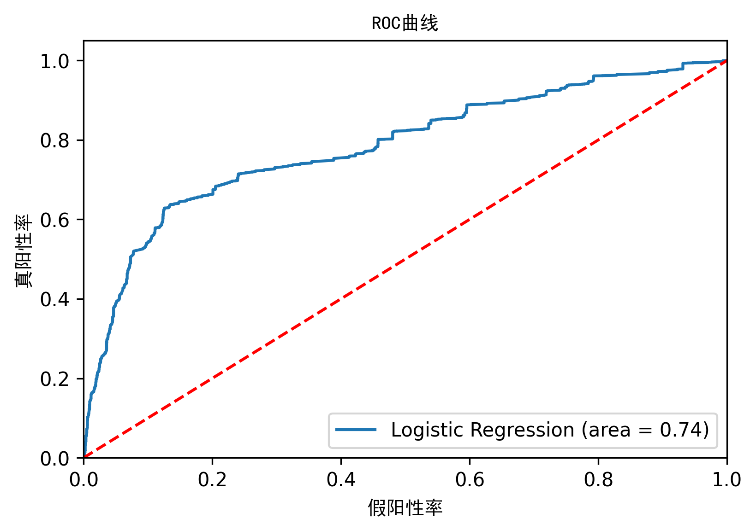
逻辑回归模型的ROC曲线
ROC曲线是另一个常用于二分类器的工具。虚线代表一个纯随机分类器的ROC曲线。一个好的分类器会尽可能远离这条线。实验中逻辑回归模型的效果远远好于随机分类器。
